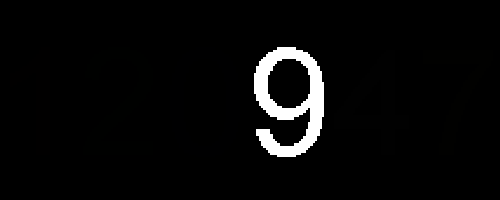Сборник задач (часть 2)

Задача 1 Как много последовательных целых положительных чисел вы можете найти, что сумма цифр (в десятичном представлении) каждого из них не делится на 13?
Замечение: Так как 49 - это первое число сумма цифр которого которое делится на 13, то целые числа от 1 до 48 удовлетворяют условию.

Задача 2 Ответ находится в этом файле: answer.zip

Задача 3 Ответ на картинке:

Задача 4 Смотря вдоль числа на его цифры, если ни одна цифра слева не превосходит цифру справа, то такое число называется возрастающим; например, 125589.

Точно также, если ни одна цифра спара не превосходит цифру слева, то такое число называется убывающим; например, 995421.

Мы будем называть число которое не является ни возрастающим ни убывающим - "прыгающим"; Например, 64783.

Очевидно что нет прыгающих чисел меньше 100, но более половины чисел меньше 1000 являются прыгающими. Число 538 является наименьшим числом для которого отношение прыгающих чисел ко всем остальным впервые достигает 50%. Удивительно, но чем дальше тем больше количество прыгающих чисел нам встречается. Когда мы достигнем числа 21780 отношение прыгающих чисел уже будет равно 90%.

Найдите наименьшее число для которого отношение прыгающих чисел будет в точности равно 99%.

Задача 5 Радикал для числа n, rad(n) - это произведение различных простых множителей для числа n. Например 1008 = 2^4*3^2*7, следовательно rad(1008) = 2*3*7 = 42.

Если мы посчитаем rad(n) для 1 <= n <= 10 и затем отсортируем их по значению rad(n) и по значению n если значения rad(n) одинаковы то мы получим:

В неотсортированном виде:
n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
rad(n) = 1, 2, 3, 2, 5, 6, 7, 2, 3, 10

В отсортированном виде:
n = 1, 2, 4, 8, 3, 9, 5, 6, 7, 10
rad(n) = 1, 2, 2, 2, 3, 3, 5, 6, 7, 10
k = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Пусть E(k) - это k-ый элемент в отсортированно n-ой колонке; например, E(4) = 8 и E(6) = 9.

Если rad(n) отсортирован для 1 <= n <= 100000, найдите E(10000).

Задача 6 Рассмотрим следующую бесконечную сумму: AF(x) = x*F(1) + x^2*F(2) + x^3*F(3) + ..., где F(k) - это k-ый элемент в последовательности Фибоначи: 1, 1, 2, 3, 5, 8, ..., которая рекуррентно определена как: F(1) = 1; F(2) = 1; F(k) = F(k-1) + F(k-2).

В этой задаче нам будут интересны значения x для который AF(x) - является целым положительным числом.

Удивительно, но AF(1/2) = 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ... = 2

Значения x для которых AF(x) - является целым положительным числом следующие:

1) x = sqrt(2)-1 AF(x) = 1
2) x = 1/2 AF(x) = 2
3) x = (sqrt(13)-2)/3 AF(x) = 3
4) x = (sqrt(89)-5)/8 AF(x) = 4
5) x = (sqrt(34)-3)/5 AF(x) = 5

Мы назовем числа AF(x) особенными если x - является рациональным числом. Особенные числа очень редкие. К примеру 10-ое особенное число равно 74049690.

Найдите 15-ое особенное число.

Задача 7 Фи-функция Эйлера F(n) определяется как число положительных целых чисел не превосходящих n которые взаимно просты с n, где 1 считается числом относительно простым по отношению ко всем числам. Таким образом F(20) = 8, так как восемь целых чисел 1, 3, 7, 9, 11, 13, 17 и 19 взаимно просты числу 20. Приведем значение функции для первых 10 чисел:

F(1) = 1, F(2) = 1, F(3) = 2, F(4) = 2, F(5) = 4,
F(6) = 2, F(7) = 6, F(8) = 4, F(9) = 6, F(10) = 4

Функция валентности v(n) определяется как число целых положительных чисел k таких что F(k) = n. Например v(8) = 5, так как только для пяти целых чисел k= 15, 16, 20, 24 и 30 F(k) = 8. В таблице приведенной ниже показаны значения функции валентности v(n) для n <= 16. (Для n отсутствующих в таблице значение равно 0).

n	v(n)	k такие что F(k)=n
1	2	1, 2
2	3	3, 4, 6
4	4	5, 8, 10, 12
6	4	7, 9, 14, 18
8	5	15, 16, 20, 24, 30
10	2	11, 22
12	6	13, 21, 26, 28, 36, 42
16	6	17, 32, 34, 40, 48, 60

Найдите значение v(2^1000), где 2^1000 - два в тысячной степени.

Задача 8 Сколькими способами можно представить число 50! в виде суммы двух или более последовательно идущих целых положительных чисел?

Задача 9 Представьте что у вас есть кристалл в форме равностороннего треугольника, длина стороны которого равна единице. При некоторых условиях кристалл начинает расти. Через минуту, две симметричные дополнительные стороны вырастают из каждого ребра треугольника. В результате получается шестиконечная звезда, длина каждой стороны которой в точности равна 1/3 от стороны из которой она появилась. По прошествии следующей минуты из каждой стороны фигуры снова появляются две стороны, длина каждой из котрых равна 1/3 от первоначальной. См. рисунки для более наглядного описания:

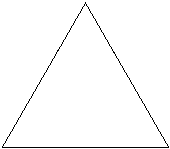
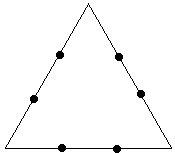
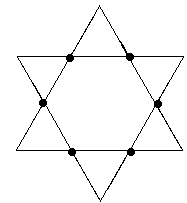
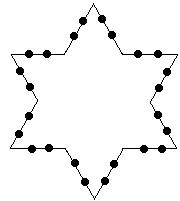
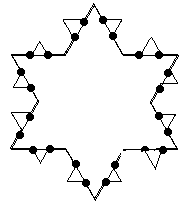
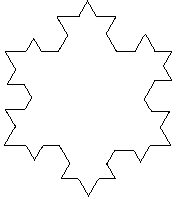
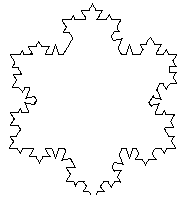
Ваша задача найти периметр фигуры (округленный до ближайшего целого) по прошествии одного часа и тридцати трех минут.

Задача 10 Ещё одна картинка:

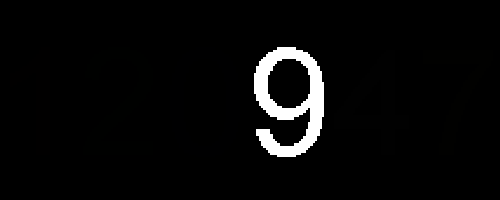
Входные данные

В данной задаче нет входных данных

Выходные данные

Выведите ответ в виде набора строчек, на отдельной строчке сначала номер задачи, затем её ответ. Если ответ будет неверным, то вы получите в результате Wrong Answer.

Начисление очков

За каждую решенную задачу вы получите ровно 1 очко (то есть максимум 10, если будут решены все 10 задач).

Пример

1 6174046
2 AnsweR
5 806257
8 51146700

Это просто пример как должны выглядеть выходные данные. Если все 4 ответа (на 1, 2, 5 и 8 задачи) правильные, то вы получите 4 очка.