8. Шарик на столе
Давным-давно в далёкой галактике металлический шарик катался по странному столу. Стол представляет собой прямоугольник, левый и правый края которого открыты, а верхний и нижний (в соответствии с видом сверху, как показано на рисунке) его края могут содержать участки с бордюрами. Стол расположен в зоне действия сильного поля, которое действует в вертикальном направлении. На рисунке направление поля показано тремя параллельными стрелками. Поле придает шарику постоянную вертикальную скорость в направлении своего действия. Шарик стартует с середины левого края стола под углом 45° относительно его нижней стороны и движется с постоянной горизонтальной скоростью. Если шарик выкатывается за пределы стола, то он сваливается с него. В этом случае он вынужден начинать свой путь сначала. Удар шарика о бордюр является абсолютно неупругим: при ударе шарик теряет свою вертикальную составляющую скорости, но его горизонтальное движение продолжается вдоль бордюра. Если при этом поле не изменит своего направления, то по достижении конца бордюра шарик падает со стола.
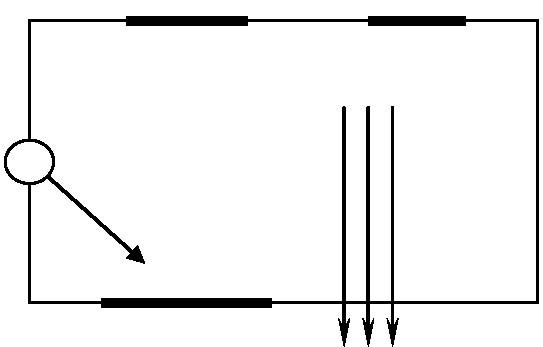
Возникает заинтересованная сторона, которая желает довести шарик до другого края стола с помощью ручных переключений поля. Вручную поле переключается мгновенно. При этом, если шарик находится в свободном движении или катится по бордюру, по направлению к которому было включено поле, то после переключения поля шарик приобретает вертикальную компоненту скорости, равную горизонтальной, и направленную к противоположной стороне стола.
Требуется придумать эффективную схему переключений поля, которая позволит минимальным количеством ручных переключений довести шарик из начальной точки на левом крае стола до правого края, не позволяя ему свалиться на своем пути.
Входные данные
В первой строке входного файла через пробел записано два целых числа L и W– длина и ширина стола (1 <= L <= 10^8, 1 <= W <= 10^9).
Во второй строке записано два целых числа N и M – количество бордюров на верхней и нижней сторонах стола соответственно (0 <= N, M <= 10^5).
В следующих N строках описываются бордюры, расположенные на верхней стороне стола. Каждый бордюр описывается на отдельной строке двумя целыми числами li и ri, которые задают горизонтальные координаты начала и конца бордюра соответственно (0 <= li < ri <= L).
В следующих M строках описываются бордюры, расположенные на нижней стороне стола в таком же формате.
Никакие два бордюра не пересекаются и не касаются. Горизонтальная координата, с которой стартует шарик, равна 0. Касание шарика бордюра в крайней его точке также считается ударом. Изначально поле направлено в сторону нижней границы стола.
Выходные данные
В первую строку выходного файла необходимо вывести единственное целое число — минимальное количество переключений поля, необходимое для того, чтобы довести шарик до правого конца стола.
Пример
input.txt
9 4
1 1
6 8
2 3
output.txt
2
Примечание: рисунок в условии не соответствует приведенному примеру.
Соревнование: XI Открытая Всесибирская олимпиада по программированию имени И.В. Поттосина 2010
Источник: http://olimpic.nsu.ru
| 