| ||||
Анализ помехоустойчивости
Во время разработки теории анализа помех в цифровых схемах, перед исследователями возникла следующая проблема. После проведенных эксперементов выяснилось, что часть узлов не может переключаться одновременно. Например известно, что если узел N переключается из состояния 0 в состояние 1, то узел K в данный момент переключится не может в сиl
3;у логических ограничений в схеме. Каждый узел переключаясь вносит некоторую помеху и эту помеху удалось количественно померить. Исследователям понадобилось придумать способ быстро измерить максимальную помеху, которую могут вызвать переключающиеся узлы.
Ученым удалось формализовать задачу следующим образом:
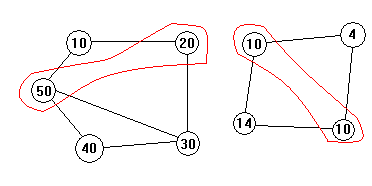
Дан граф G = (V, E, w) состоящий из набора вершин V, набора ребер Входные данныеt – число тестов [t <= 60] Выходные данныеДля каждого теста выведите на отдельной строчке MaxWeight – вес максимального независимого набора вершин для данного графа [ 0 <= MaxWeight <= 10^9]. ПримерВходные данные: 2 5 6 10 20 30 40 50 1 2 1 5 2 3 3 4 3 5 4 5 4 4 10 4 10 14 1 2 2 3 3 4 4 1 Выходные данные: 70 20 Иллюстрация к тестам:
|
||||
| ||||
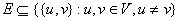 , и весовой функции W, такой что
, и весовой функции W, такой что 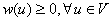 и
и 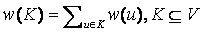 . Для
. Для 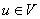 и
и 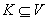 , N(u) и N(K) означают соседний набор вершин u и K соответсвенно, формально определенные так:
, N(u) и N(K) означают соседний набор вершин u и K соответсвенно, формально определенные так: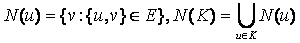
 называется независимым. В данной задаче необходимо найти такой набор независимых вершин B что w(B) = max{w(S)}, где S принадлежит множеству всех независимых наборов вершин графа G.
Известно также, что плотность ребер в графе находится между 20 и 90%.
называется независимым. В данной задаче необходимо найти такой набор независимых вершин B что w(B) = max{w(S)}, где S принадлежит множеству всех независимых наборов вершин графа G.
Известно также, что плотность ребер в графе находится между 20 и 90%.