Сборник Задач (Часть 3)

Задача 1 Используя комбинацию из блоков разного цвета и разной длины: 1, 2, 3 и 4 можно заполнить ряд длинной 5 ровно 15 различными способами:

Сколькими способами можно заполнить ряд длинной 50?

Задача 2 Шестиугольная ячейка с числом 1 находится в центре кольца состоящего из 6 других ячеек той же формы. Нумерация ячеек начинается с "12 часов" начиная с 2 и заканчивая 7, против часовой стрелки. Новые кольца добавляются таким же образом и имеют нумерацию от 8 до 19, от 20 до 37 и от 38 до 61, и.т.д. На рисунке ниже показаны первые три кольца:

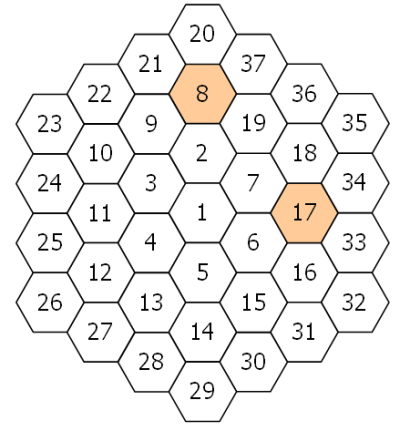
У каждой ячейки на этом поле есть 6 соседей. Найдя разницу между ячейкой n и её соседями, определим функцию, F(n), которая означает число соседей, разница с которыми является простым числом. Например, для ячейки 8 разницы с соседями: 12, 29, 11, 6, 1, 13, т.е. F(8) = 3. Аналогично, для ячейки 17, разницы с соседями равны: 1, 17, 16, 1, 11 и 10, т.е. F(17) = 2. Можно доказать, что максимальное значение для F(n) равно 3. Если все ячейки, для которых F(n) = 3 расположить в возрастающем порядке, то 10 элементом в этом ряде будет 271. Найдите 2000-ый элемент.

Задача 3 Пусть P(A) равно сумме элементов в множестве A размера n. Назовем P(A) специальной суммой, если для любых двух не пустых непересекающихся подмножеств B и C выполняются следующие свойства:

1) P(C) != P(B), т.е. сумма подмножеств не может совпадать
2) Если B содержит больше элементов, чем C, то P(B) > P(C)

В этой задаче положим, что заданное множество содержит n строго возрастающих чисел и оно уже удовлетворяет второму свойству.

Удивительно, но среди 25 возможных пар подмножеств для множества, у которого n=4, только одна пара должна быть проверена на совпадение (см. 1 свойство). Аналогично, для n=7 всего 70 из 966 пар должны быть проверены на совпадение. Для n=12 сколько пар из 261625 должны быть проверены на совпадение?

Задача 4 Найдите наименьшее число больше 15, куб которого состоит только из цифр являющихся простыми числами {2, 3, 5, 7}.

Задача 5 Титаническим числом называется число, для десятичной записи которого требуется 1000 или более значащих цифр. В этой задаче необходимо найти минимальное титаническое число, которое может быть представлено в форме: p^q, где знак ^ означает возведение в степень, а p и q являются простыми числами. Ответ необходимо вывести в форме: X-q, где X - последние 10 цифр титанического числа, а q показатель степени. Например: 8765839202-97

Задача 6 Найдите наименьшее натуральное число N для которого серия (N-k)/k является простыми числами для всех k=1,...n при n = 11. Для n=4 число N=12, проверим: (12-1)/1 = 11, (12-2)/2 = 5, (12-3)/3 = 3, (12-4)/4 = 2.

Задача 7 Вы играете в игру, в которой можете попросить ведущего назвать число. Каждое названное ведущим вещественное число является независимым случайным и равномернораспределенным на интервале между 0 и 1. После того как вам назвали число, вы можете либо попросить следующее число, либо остановиться. Когда вы остановитесь, вашим счетом будет сумма всех чисел, которые вам назвал ведущий. Пусть 0 < x < 1 и положим, вы пытаетесь получить счет на промежутке от x до 1. Какова вероятность вашего успеха при условии использования наилучшей стратегии? Найдите численное значение вероятности для x=0.334568 и выведите его в форме x.xxxxxx - где вместо x округленное до 6 знаков после запятой значение вероятности.

Задача 8 Найдите количество целых чисел на интервале 1 < n < 10000000, для которых n и n+1 имеют одно и то же число положительных делителей. Например, 14 делится на 1, 2, 7, 14, а 15 делится на 1, 3, 5, 15.

Задача 9 Расшифруйте надпись на картинке:

Выведите её строчными английскими буквами без пробелов.

Задача 10 Представим, что у вас в наличии оказалась небольшая программа, защищенная "ключом активации", который зависит от введенного имени. Реализация защиты этой программы на Си приведена ниже. Программа спрашивает имя и пароль, проверяет его и выводит "Верно" или "Не верно".

#include <stdio.h>

unsigned int code (unsigned int arg, int p, int n)
{
	unsigned int r = 1;
	for(; p >= 1; p--)
		r = (r*arg)%n;
	return r;
}

void main ()
{
	unsigned int e = 35467, n = 54031, pwd;
	char name[256];
	unsigned int hash, x;

	printf("Name: "); 
	scanf("%s", name);
	
	printf("Password: "); 
	scanf("%d", &pwd);

	hash = 0;
	for (x = 0; ; x++){
		if (name[x] == 0)
			break;
		hash += name[x];
	}

	if (code(pwd, e, n) == hash)
		printf("Верно!\n");
	else 
		printf("Не верно\n");
}

Задача заключается в том, что бы найти правильные пароли для спиcка имен, заданных в файле nicks.zip (~330 Kb). Ответом для задачи будет сумма всех полученных вами паролей.

Входные данные

В данной задаче нет входных данных

Выходные данные

Выведите ответ в виде набора строчек, на отдельной строчке сначала номер задачи, затем её ответ. Если ответ будет неверным, то вы получите в результате Wrong Answer.

Начисление очков

За каждую решенную задачу вы получите ровно 1 очко (то есть максимум 10, если будут решены все 10 задач).

Пример

1 6174046
2 AnsweR
5 806257
8 51146700

Это просто пример как должны выглядеть выходные данные. Если все 4 ответа (на 1, 2, 5 и 8 задачи) правильные, то вы получите 4 очка.